016 逻辑的几何学一种简单的逻辑方法

type

Post

status

Published

date

Aug 17, 2022

slug

016

summary

逻辑学很复杂，这本书作者提供了一个简单的用几何来表示逻辑的方法——逻辑的几何学

前言

大学中有一本非常重要的书——《马克思主义基本原理》[1]，启发了我认识世界的角度和方法——唯物辩证法和认识论。这些对于解决问题非常有帮组，比如说：

重点论：抓住最重要的矛盾

两点论：抓住矛盾的两个方面

实事求是：从实践中发现事物的联系，而不是从脑袋中空想。

……

这本书归纳出了四对辩证思维方法：归纳和演绎，分析和综合，逻辑和历史，抽象和具体。而《逻辑的几何学》[2]这份手稿讲的就是分析和综合这一对辩证思维如何利用几何的方法来表示。读完了之后，加深了对两种逻辑方法的认识，并且得到了一种清晰有效解决现实问题的方法。

1. 分析逻辑和综合逻辑

因为《逻辑的几何学》[2]是一本讲逻辑的书本，所以在这本书中，分析和综合作为一种逻辑方法，是作为一个专用的名词来使用。于是引出接下来两个问题：那么什么是分析逻辑，什么是综合逻辑呢？两种逻辑背后的规律是什么呢？

1.1. 两种逻辑是什么？

什么是分析逻辑，什么是综合逻辑？有很多种回答，其中回答最好的，应该是我们的教科书中回答，《马克思主义基本原理 2015版》[1]对两者做了详细的定义：

分析，就是在思维中把认识对象分解为各个部分、方面、要素，以便分别加以研究的思维方法。

综合，就是在思维中把对象的各个本质的方面按其内在联系有机地结合成一个统一的整体。

image-20220812144628966

图 1两种逻辑和研究对象的关系

图 1形象化说明了分析和综合两种逻辑方法是如何用来研究具体的事物：先将事物划分为多个方面，详细研究明白后，再将事物有机统一起来。从而达到对事物的本质的、内在的、一般的联系的认知。

1.2. 两种逻辑的成立法则

分析逻辑来源于亚里士多德在《范畴篇》[11]的陈述：一件东西不可能在同一时间、就统一方面而言，既“是”又“不是”。既事物之间不能够互相矛盾，这条被称作“不矛盾律”。符号表示的话 A ≠ − A 基于“不矛盾律”，那么接下来就必须要让一个东西只能是它，而不能够为它物，这就是“同一律”。符合表示的话为 A = A 比如说“科学”一词便是基于上述的逻辑而产生的：“科学”，自然太复杂，分“科”而“学（研究）”，从而去研究自然。因此化学就是化学，物理就是物理，化学不是物理，物理不是化学。所以分析逻辑基于两条法则：“不矛盾律”和“同一律”。那么综合逻辑于此相反，所以其规律可以讲上述的两条法则反向使用，即“矛盾律”和“不同一律”。符合表示为 A = − A

A ≠ − A

突然间一听觉得有点问题，怎么能够这样呢？那么下面请看庄子所写《齐物论》[12]片段：

物无非彼，物无非是。自彼则不见，自知则知之。故曰：彼出于是，是亦因彼。彼是方生之说也。虽然，方生方死，方死方生；方可方不可，方不可方可；因是因非，因非因是。是以圣人不由而照之于天，亦因是也。是亦彼也，彼亦是也。彼亦一是非，此亦一是非，果且有彼是乎哉？果且无彼是乎哉？彼是莫得其偶，谓之道枢。枢始得其环中，以应无穷。是亦一无穷，非亦一无穷也。故曰：莫若以明。

“方生方死，方死方生；方可方不可，方不可方可；因是因非，因非因是。”不符合上述“矛盾律”和“不同一律”吗？但是我们读不懂庄子在说什么，因为这种逻辑法则，暂时我们不明白。这就引出了第三个问题，两种逻辑的目的是什么呢？这在下一节进行讲解。

总的来说，分析逻辑基于“不矛盾律”和“同一律”，综合逻辑基于“矛盾律”和“不同一律”。

1.3. 两种逻辑方法的目的？

分析逻辑，对象是明确的，只是我们暂时还不能够认识，所以需要分析，说明分析逻辑的目的是为了深入了解和认识在我们认知范围之内的事物。现代的科学均是如此。

那么综合逻辑呢？再一次去看看《齐物论》[12]，发现这是为了描述“道”或者说“物”。这东西太抽象，超出了我们的认知范围，所以这种方法是为了在我们认知范围内来描述超出我们认知范围的事物。

2. 两种逻辑方法与几何

如果想要让逻辑和几何相关，那么必须要用数学的语言来描述这两种方法。

2.1. 两种逻辑方法各自能够产生多少成分？

于是作者提出了一下的方法：既然分析逻辑方法是将事物划分为多个方面，那么简单一点，一次仅仅划分为2，正反两方面，使用“+”和“-”来表示呢？很明显，划分的层次越多，成分越多。

表格 1 分析逻辑方法的划分阶数

阶数(n)

数目S

成分

点

+, -

++, +-, -+, –

……

所以，分析逻辑能够划分的数目和阶数相关，满足以下方程： S = 2n

那么综合逻辑呢？综合逻辑是为了认识超越认知范围的事物，所以除了“+”和“-”之外，会产生一个神秘项“x”，那么一次划分便会产生三项。

表格 2 综合逻辑方法的划分阶数

阶数(n)

数目S

表达式

点

+, -, x

++, +-, +x, -+, –, -x x+, x-, xx

……

所以，分析逻辑能够划分的数目和阶数相关，满足以下方程： S = 32

2.2. 特定名词

由于上述产生了很多的东西，那么便直接从数学中借来内容来说明这些东西。

表达式（expression）：表格 1和表格 2中第三列中的内容，如“xx”、“++”、“–”等

术语（term）：组成成分的单个元素，如“+-”当中的“+”和“-”

级别（level）：划分的次数，表格 1和表格 2中第1列中的内容

3. 分析逻辑方法

按照上面的分类，分析逻辑方法[10, 3]可以划分为多个级别：

一级分析关系1LAR（1st level Analysis Relation）对应于两个表达式

二级分析关系2LAR（2ed level Analysis Relation）对应于四个表达式

三级分析关系3LAR（3rd level Analysis Realtion）对应于八个表达式

……

下面进行详细的展开，看看其和几何的关系。

3.1. 一级分析关系1LAR

由于一级分析关系对应于两个内容：正好一正一反，作者选取了最常见的两个符号“+”和“-”来代替这两个内容。如何排布这两种关系呢？

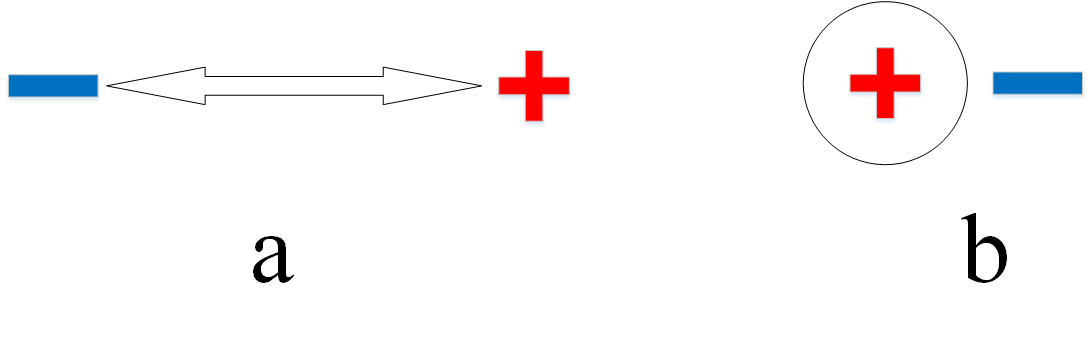
image-20220812144653286

图 2 一级分析关系1LAR

图 2 一级分析关系1LAR是一级分析关系1LAR如何几何来图形化表示。当两种力量势均力敌的时候，力量均等，使用图 2 一级分析关系1LARa来表示，如各种游戏（象棋、围棋、lol等）开局的时候的状态。当其中一种力量占上风的时候呢？这样一种力量比较弱小，另外一种力量比较强大，因而强大的会包裹弱小的，使用图 2 一级分析关系1LARb来表示。在1LAR当中，两者是完全矛盾，不相容的，这里使用双箭头来进行表示。

image-20220812144715965

图 3 《论持久战》中敌我力量变化的三个阶段（“+”表示“中国军队”，“-”表示“日本军队”）：a，敌强我弱，被敌军包围；b，力量相持，包围和反包围；c：敌弱我强，战略决胜阶段

图 3描绘了《论持久战》[9]中所预测的敌我力量的变化。初始阶段，中国军队弱小，被日本帝国主义分割包围；相持阶段，随着农村革命根据地的建立，双方力量势均力敌，城市分割农村，农村包围城市；决胜阶段，经过长期的斗争，各个根据地连成一片，完全将日本军队包围在孤立的城市当中。

3.2. 二级分析关系2LAR

2LAR产生了四个表达式（++, +-, -+, –），相对于1LAR，关系的类型多了一种，即表达式中的两个术语，一个相同，一个不同。于是4个表达式产生的6个相互关系可以分为一下两组。

矛盾关系[2]：术语完全不同，“++”和“–”，“+-”和“-+”；使用双箭头；

反对关系[2]：术语部分相同，“++”和“+-”，“++”和“-+”，“–”和“+-”，“–”和“-+”；使用单箭头；

那么，这种关系应该怎么画呢？

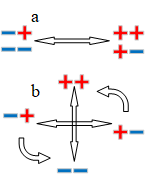
image-20220812144750179

图 4 矛盾对立产生的2LAR

作者从图 2(a)出发，将双箭头旋转90°，会产生一个十字。但是各自两端产生什么呢？

图 4是以矛盾关系为基础产生的2LAR。假设两端完全矛盾，即“+”端产生“++”和“+-”，“-”端产生“-+”和“–”，旋转90°后，便产生了一个十字。这个便是我们日常生活中最常见的图形。

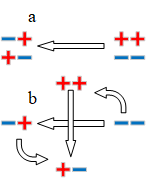
image-20220812144807587

图 5 以反对关系产生的2LAR

图 5是以反对关系为基础产生的2LAR。假设“+”端是“纯粹表达式”，即“+”端产生“++”和“–”；“-”端是“混合表达式”产生“-+”和“+-”，旋转90°后，便产生了一个十字。

当然呢，这个也可以转换到正方形和圆形上。如果想要使用圆形来表达，在外部画一个圆，将四个表达式包围，变成一个圆形；如果想要使用正方形，那么将临近的表达式相互连接起来，变成一个正方形。下面看一下其转换呈正方形的状态。

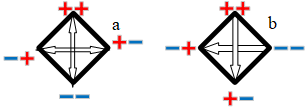
image-20220812144823509

图 6 正方形表示的2LAR

图 6表示正方形结构的2LAR。其中发现，矛盾关系的图 6a相对来说更加直观和清晰明了，正如我们的先天太极图便是此种情况；而反对关系的图 6b相对来说没有那么直观，但是可以图 5b便是那么直观。

所以，以矛盾关系为基础的2LAR使用正方形来表示，以反对关系为基础的2LAR使用十字来表示。

3.3. 二级分析关系2LAR的补充说明

由于2LAR根据划分的关系不同，产生了两张图，那么有下面的问题：

以矛盾关系为基础得到的图 4b有没有反对关系呢？

以反对关系为基础得到的图 5 以反对关系产生的2LARb中有没有矛盾关系呢？

2LAR会产生4个表达式，两两相连，会产生六对关系，其中两对矛盾关系，四对反对关系，如果全部前加上，那就能够回答上面的问题。

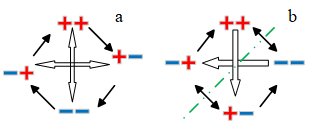
image-20220812144834147

图 7 2LAR关系的拓展形式：a，增加反对关系；b，增加反对关系和矛盾关系

图 7a中增加了四对反对关系，所以形成了一个顺时针的循环，说明矛盾关系可以通过中间体来相互转换。图 7b增加了两个反对关系和两个矛盾关系，绿线是矛盾关系的的分界线，如果将两边分成两组的话，那么任何一组都是既有矛又有盾的组，这样才是势均力敌。

3.4. 三级分析关系3LAR

三阶分析关系，在二阶的基础上进行改进，其中以矛盾关系为基础得到的三阶分析关系图，可以将图 7a进行划分，然后逆时针旋转45°，便可以得到先天太极八卦图。其中“+”代表阳，变成八卦中的“—”；“-”代表阴，变成八卦中的“- -”。

image-20220812144902437

图 8 先天太极八卦图

至于如何产生以反对关系为基础的3LAR图，暂时还没有研究明白。当然，不仅仅是这种，还可以产生正方体，每个顶点代表一个表达式。

4. 综合逻辑方法

按照表格 2，综合逻辑方法可以划分为多个级别：

一级综合关系1LSR（1st level Synthesize Relation）对应于3个表达式

二级综合关系2LSR（2ed level Synthesize Relation）对应于9个表达式

三级综合关系3LSR（3rd level Synthesize Realtion）对应于27个表达式

……

下面进行详细的展开，看看其和几何的关系。

4.1. 一级综合关系1LSR

一级综合关系对应于三个表达式：+、-和x，如果想要让三者排列完整，那么等边三角形就非常合适。

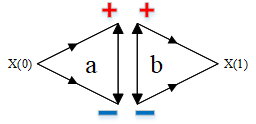
image-20220812144916828

图 9 两种综合的形式：a，原初的综合；b，最终的综合

图 9表示综合的两种形式，前者为原初的综合，即事物一分为二；后者表示最终的综合，经过对两部分内容的深入研究，经过去粗取精、去伪存真、由表及里、由此及彼的过程，从而得到已经经过认识的新的对象X(1)。这个时候，它既是X，但是不是X(0)所代表的没有认知的X，而是已经对内部结构有了深入了解的X(1)。

当然，图 2b也可以表示综合关系，中间的那条线表示X，但是没有三角形直观形象，所以作者推荐使用图 9的形式[10]。

现实生活中的综合，比如说一对父母生出了一个孩子x。但是这个孩子在出生前是没有办法被认知的：不知道是男还是女，不知道是能够正常出生还是中途夭折，不知道是正常还是残疾……

4.2. 二级综合关系2LSR

二级的综合关系，有九个表达式，那么该如何进行表述呢？对待九个表达式，每个表达式需要和其他两个表达式相连，应该存在十二根三角形。这个太复杂了，暂时没有想明白，作者推荐了一张图——九型人格[8]。

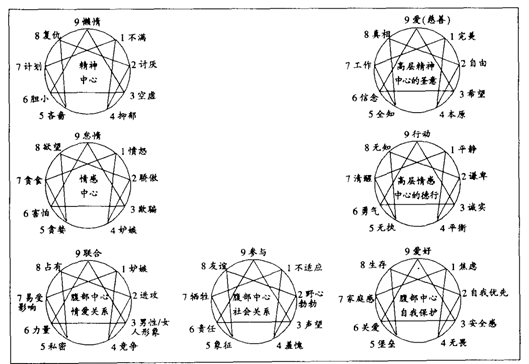
image-20220812144933820

图 10 九型人格（来自于《九型人格》）

图10是2LSR的一种表达形式，但是暂时没有看明白是如何绘制出来的。如果大家能够看明白的话，希望给予一点点帮组呀!

5. 复合关系

两种方法不是泾渭分明的关系，而是可以相互协作，用来处理更加复合关系CR（Complex Relation）。下面提出几个作者提到的例子。当然其中产生的数目是相乘的关系。

6项表达式复合关系6CR（6 Complex Relation）= 1LAR + 1LSR

12项表达式复合关系12CR（12 Complex Relation） = 2LAR + 1LSR

5.1. 6CR = 1LAR + 1LSR

1LAR有两个表达式，1LSR有三个表达式，两者相乘，共有六个表达式。

image-20220812145258611

图 11 6CR的图形表达

这样的话，就会形成两个三角形。这个就是古代的六芒星，又称作大卫之星。根据这个，我形成了一个道德完善计划，可以见一下链接https://zhuanlan.zhihu.com/p/518835896

5.2. 12CR = 2LAR + 1LSR

1LAR有四个表达式，1LSR有三个表达式，两者相乘，共有12个表达式。这样的话，可以使用圆形来表达。

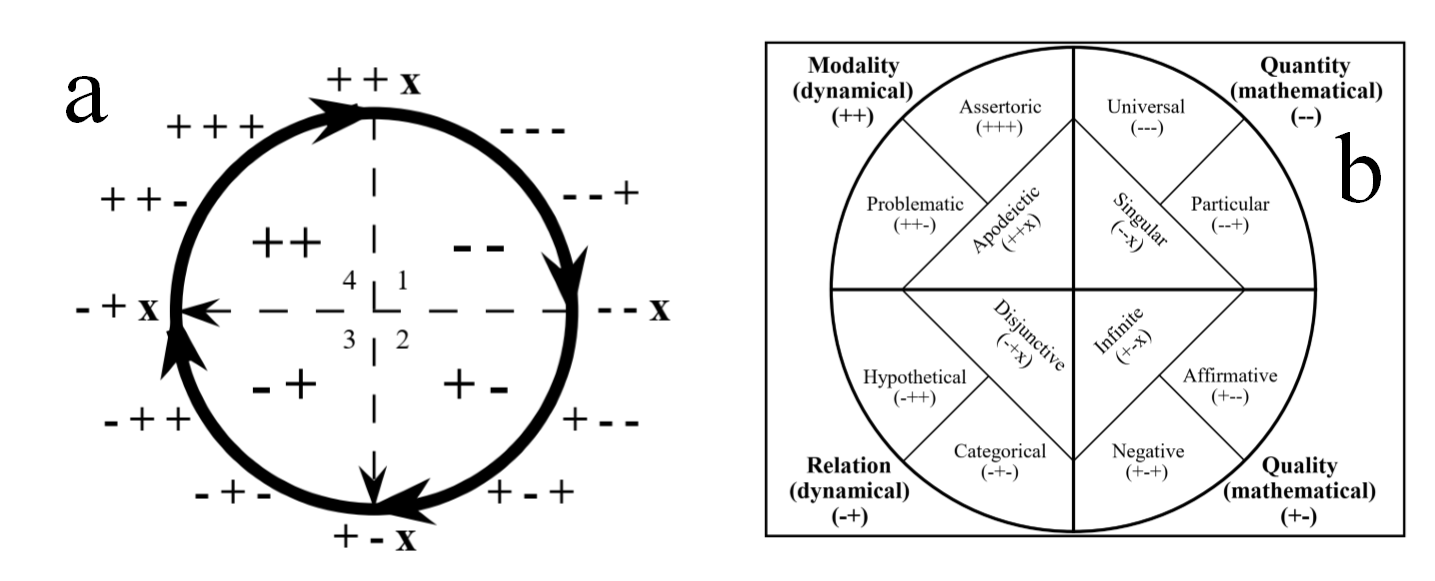
image-20220812145321580

图 12 12CR关系的表达：a，表达式放置在圆周上；b，表达式按照圆的面积划分

图 12是利用圆形来表达12CR关系，前者放置到圆周上，后者放置在圆的内部面积上。符合12CR关系有以下的例子：

一年有12个月，四个季度，每个季度三个月

夸克有12种

电磁力有12中（Maxwell发现）

……

5.3. 对六十四卦的新解

作者同样对《易经》[4-7]当中的六十四卦进行了重新的整理，整理出了两张和正常不一样的图形。

image-20220812145337478

图 13 逻辑的几何学角度下的易经：a，6LAR视角的易经；b，混合视角的易经

图 13是应用逻辑的几何学来对易经进行重新排布。其中前者是6级分析关系视角下的易经排列，像曼陀罗花一样；后者是利用混合关系来排布的易经，2LAR+2LAR+（3个2LAR和一个1LSR）组成。

6. 结语

通过阅读《逻辑的几何学》手稿，发现收获良多。当然由于这本书当中缺少一些必要的图形，所以阅读起来特别困难。连蒙带猜，写了以上的读后感。2022.08.08给作者发了一封邮件询问关于图片的事情，作者说他会在完成手边的工作之后写《逻辑的几何学》，同时建议我去看他已经出版的其他内容，如The Tree of Philosophy。

下面是作者的其他出版物所在的网址：

hkbu.academia.edu/StephenPalmquist

www.researchgate.net/profile/Stephen_Palmquist

orcid.org/0000-0002-9448-8793

www.hkbu.edu.hk/~ppp

7. 参考文献

[1] 《马克思主义基本原理概论》教材编写课题组. 马克思主义基本原理概论（2015年修订版）[M]. 北京:高等教育出版社,2015

[2] PALMQUIST S. The Geometry of Logic[M]. http://staffweb.hkbu.edu.hk/ppp/gl/toc.html:unpublished.

[3] PALMQUIST S 1992. Analysis and Synthesis in the Geometry of Logic[J]. Indian Philosophical Quarterly, 19.

[4] PALMQUIST S 2011. Architectonic Reasoning and Interpretation in Kant and the Yijing[J]. Journal of Chinese Philosophy, 38: 569-583.

[5] PALMQUIST S 2011. Introduction: Levels of Perspectives in Kant and Chinese Philosophy[J]. Journal of Chinese Philosophy, 38: 505-508.

[6] PALMQUIST S 2012. Mapping Kant’s Architectonic onto the Yijing Via the Geometry of Logic[J]. Journal of Chinese Philosophy, 39: 93-111.

[7] PALMQUIST S 2015. Twelve Basic Philosophical Concepts in Kant and the Compound Yijing[J]. Journal of Chinese Philosophy, 42: 143-162.

[8] 海伦·帕尔默著，徐扬译. 九型人格[M]. 北京:华夏出版社,2006

[9] 毛泽东. 毛泽东选集[M]. 北京:人民出版社,1991

[10] 庞思奋. 哲学之树[M]. 广西:广西师范大学出版社,2005

[11] 亚里士多德著，方书春译. 范畴篇解释篇[M]. 北京:商务印书馆,2003

[12] 庄周著方. 庄子[M]. 北京:中华书局,2010